De onderstaande tabel geeft een driepersoonsspel $(N,v)$.
| $S$ | $\{1\}$ | $\{2\}$ | $\{3\}$ | $\{1,2\}$ | $\{1,3\}$ | $\{2,3\}$ | $\{1,2,3\}$ |
| $v(S)$ | $0$ | $0$ | $0$ | $6$ | $7$ | $8$ | $10$ |
We zullen grafisch laten zien dat dit spel een lege core heeft. Allereerst schrijven we uit aan welke (on)gelijkheden een verdeling $x$ die in de core van dit spel ligt moet voldoen:
$$\begin{align}
x_{1}+x_{2}+x_{3} &=v(\{1,2,3\})=10, \\
x_{1} &\geq v(\{1\})\phantom{,2,3}= \phantom{1}0,\\
x_{2} &\geq v(\{2\})\phantom{,1,3}=\phantom{1}0,\\
x_{3} &\geq v(\{3\})\phantom{,1,2}=\phantom{1}0,\\
x_{1}+x_{2} &\geq v(\{1,2\})\phantom{,3} = \phantom{1}6,\\
x_{1}+x_{3} &\geq v(\{1,3\})\phantom{,2}= \phantom{1}7,\\
x_{2}+x_{3} &\geq v(\{2,3\})\phantom{,1}= \phantom{1}8.
\end{align}$$
We gaan nu in een plaatje kijken welke punten er mogelijk in de core kunnen liggen. Mogelijke core-elementen liggen in de driehoek $x_1+x_2+x_3=10$ met $x_1\geq 0$, $x_2\geq0$ en $x_3\geq 0$, omdat elke speler zonder samenwerking 0 kan verdienen. Dit zijn dus alle verdelingen die in de driehoek met als hoekpunten $(10,0,0)$, $(0,10,0)$ en $(0,0,10)$ liggen, zie het plaatje hieronder.
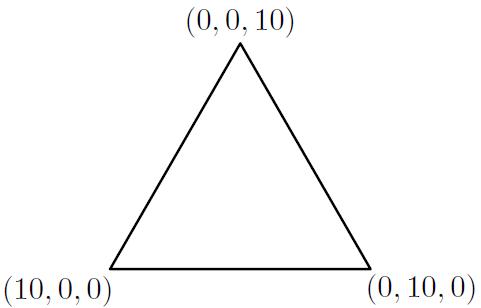
Voordat we naar de overige ongelijkheden gaan kijken, tekenen we eerst de lijnstukken $x_1+x_2=v(\{1,2\})=6$, $x_{1}+x_{3}= v(\{1,3\})=7$ en $x_{2}+x_{3}=v(\{2,3\})=8$ in deze driehoek. Het lijnstuk $x_1+x_2=v(\{1,2\})=6$ heeft bijvoorbeeld als hoekpunten $(6,0,4)$ en $(0,6,4)$. In het plaatje hieronder zijn deze drie lijnstukken getekend.

Bekijk nu het plaatje hieronder.
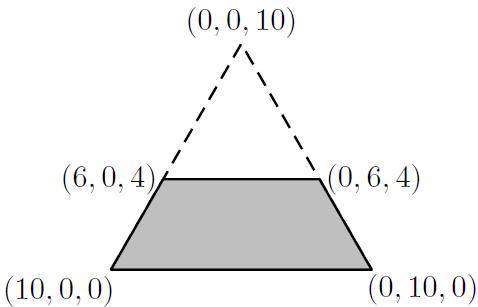
Alle verdelingen buiten het lichtgrijze gebied (dat als hoekpunten $(6,0,4)$, $(0,6,4)$, $(10,0,0)$ en $(0,10,0)$ heeft) kunnen niet in de core liggen, omdat buiten dit gearceerde gebied geldt dat $x_1+x_2<6$. Verdelingen die in de core liggen, moeten dus in het lichtgrijze gebied liggen.
Bekijk dit lichtgrijze gebied nog eens in het plaatje hieronder.
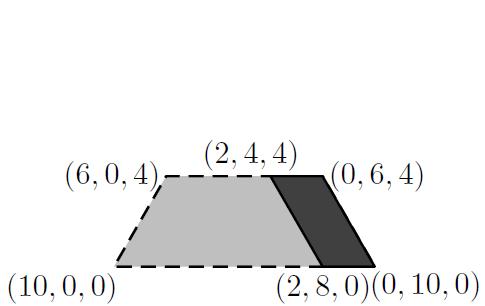
Verdelingen buiten het donkergrijze gebied, (dat als hoekpunten $(2,4,4)$, $(0,6,4)$, $(0,10,0)$ en $(2,8,0)$ heeft) kunnen niet in de core liggen, omdat voor deze verdelingen geldt $x_2+x_3<8$. Maar als we de verdelingen in het donkergrijze gebied bekijken dan zien we dat deze ook niet in de core kunnen liggen, omdat voor die verdelingen geldt dat $x_1+x_3<7$. Geen enkele verdeling voldoet dus aan alle core condities en dus is de core in dit geval leeg.

