We saw that the area $O(f,a,b)$ of the region below the graph of a non-linear function $f(x)$ can be approximated by summing the area of the best-fitting bars under the graph, hence, $O=O_1+O_2+\ldots O_n$. The more bars we use (hence, the larger $n$), the better the approximation of the area. We now investigate the relation between this approximation and integrals.
Consider the previously used example with three strips.
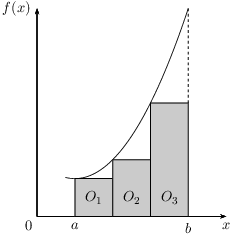
The interval $[a,b]$ is then split into three subintervals (of the same size) $[a,x_1]$, $[x_1,x_2]$ and $[x_2,b]$. The area of the first bar can be calculated as follows: $O_1=f(a)\cdot (x_1-a)$. In the same way we obtain the areas of the second $O_2=f(x_1)\cdot (x_2-x_1)$ and third bar $O_3=f(x_2)\cdot (b-x_2)$. Conclusion:
$$O\approx f(a)(x_1-a)+f(x_1)(x_2-x_1)+f(x_2)(b-x_2)\quad(1).$$
Derivative: From Chapter 2 we know that for a derivative $y'(x)$ of a function $y(x)$ it holds that
$$\dfrac{y(x+\Delta x) - y(x)}{\Delta x} \approx y'(x).$$
When we replace in this expression the function $y(x)$ by an antiderivative $F(x)$ then we obtain
$$\dfrac{F(x+\Delta x) - F(x)}{\Delta x} \approx F'(x)=f(x),$$
which we can rewrite to
$$F(x+\Delta x)-F(x)\approx f(x)\Delta x\quad (2).$$
Relation to integral: Consider equation (2). If we take in this expression $x=a$ and $\Delta x=x_1-a$, such that $x+\Delta x=x_1$, then
$$F(x_1)-F(a)\approx f(a)(x_1-a)=O_1.$$
Taking $x=x_1$ and $\Delta x=x_2-x_1$, such that $x+\Delta x=x_2$, gives
$$F(x_2)-F(x_1)\approx f(x_1)(x_2-x_1)=O_2.$$
Taking $x=x_2$ and $\Delta x=b-x_2$, such that $x+\Delta x=b$, gives
$$F(b)-F(x_2)\approx f(x_2)(b-x_2)=O_3.$$
Hence, we can rewrite equation (1) as
$$O\approx O_1+O_2+O_3\approx (F(x_1)-F(a))+(F(x_2)-F(x_1))+(F(b)-F(x_2))=F(b)-F(a)\quad (3).$$
Since $F(b)-F(a)=\int_a^b f(x)dx$ we have an approximation for the integral. Note that this approximation improves by increasing the number of bars. If the number of bars becomes infinite we can replace the $\approx$-signs by $=$-signs. This holds for both equation (2) and equation (3).
Conclusion: The area of the region enclosed by the graph of the function $f(x)$, the $x$-axis and the lines $x=a$ and $x=b$ is equal to the integral $\int_a^b f(x)dx$.
Consider the previously used example with three strips.

The interval $[a,b]$ is then split into three subintervals (of the same size) $[a,x_1]$, $[x_1,x_2]$ and $[x_2,b]$. The area of the first bar can be calculated as follows: $O_1=f(a)\cdot (x_1-a)$. In the same way we obtain the areas of the second $O_2=f(x_1)\cdot (x_2-x_1)$ and third bar $O_3=f(x_2)\cdot (b-x_2)$. Conclusion:
$$O\approx f(a)(x_1-a)+f(x_1)(x_2-x_1)+f(x_2)(b-x_2)\quad(1).$$
Derivative: From Chapter 2 we know that for a derivative $y'(x)$ of a function $y(x)$ it holds that
$$\dfrac{y(x+\Delta x) - y(x)}{\Delta x} \approx y'(x).$$
When we replace in this expression the function $y(x)$ by an antiderivative $F(x)$ then we obtain
$$\dfrac{F(x+\Delta x) - F(x)}{\Delta x} \approx F'(x)=f(x),$$
which we can rewrite to
$$F(x+\Delta x)-F(x)\approx f(x)\Delta x\quad (2).$$
Relation to integral: Consider equation (2). If we take in this expression $x=a$ and $\Delta x=x_1-a$, such that $x+\Delta x=x_1$, then
$$F(x_1)-F(a)\approx f(a)(x_1-a)=O_1.$$
Taking $x=x_1$ and $\Delta x=x_2-x_1$, such that $x+\Delta x=x_2$, gives
$$F(x_2)-F(x_1)\approx f(x_1)(x_2-x_1)=O_2.$$
Taking $x=x_2$ and $\Delta x=b-x_2$, such that $x+\Delta x=b$, gives
$$F(b)-F(x_2)\approx f(x_2)(b-x_2)=O_3.$$
Hence, we can rewrite equation (1) as
$$O\approx O_1+O_2+O_3\approx (F(x_1)-F(a))+(F(x_2)-F(x_1))+(F(b)-F(x_2))=F(b)-F(a)\quad (3).$$
Since $F(b)-F(a)=\int_a^b f(x)dx$ we have an approximation for the integral. Note that this approximation improves by increasing the number of bars. If the number of bars becomes infinite we can replace the $\approx$-signs by $=$-signs. This holds for both equation (2) and equation (3).
Conclusion: The area of the region enclosed by the graph of the function $f(x)$, the $x$-axis and the lines $x=a$ and $x=b$ is equal to the integral $\int_a^b f(x)dx$.

