Consider the function $f(x)=-x^2+3x-2$. We determine the area of the region enclosed by the graph of $f(x)$, the $x$-axis and the lines $x=0$ and $x=2$.
We first of all investigate on which (sub)intervals the function $f(x)$ is non-negative or non-positive. For this we determine the zeros of $f(x)$.
$$f(x)=0\Leftrightarrow -x^2+3x-2=0\Leftrightarrow -(x-1)(x-2)=0\Rightarrow x=1\mbox{ or } x=2.$$
On the interval $[0,1]$ it holds that $f(x)\leq 0$ and on the interval $[1,2]$ it holds that $f(x)\geq 0$, see the following graph.
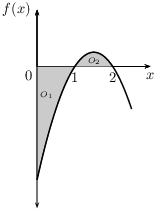
The total area $O(f,0,2)$ of the shaded region is equal to $O_1+O_2$. According to the theorem regarding integrals and areas we can express this area in terms of integrals, that is
$$O_1+O_2=-\int_0^1 (-x^2+3x-2)dx+\int_1^2 (-x^2+3x-2)dx.$$
An antiderivative of $f(x)$ is the function $F(x)=-\frac{1}{3}x^3+\frac{3}{2}x^2-2x$. Now we are able to calculate the desired integrals.
$$\begin{align}
\int_0^1 (-x^2+3x-2)dx&=[-\frac{1}{3}x^3+\frac{3}{2}x^2-2x]_{x=0}^{x=1}=(-\frac{1}{3}+\frac{3}{2}-2)-0=-\frac{5}{6}\\
\int_1^2 (-x^2+3x-2)dx&=[-\frac{1}{3}x^3+\frac{3}{2}x^2-2x]_{x=1}^{x=2}=(-\frac{8}{3}+6-4)-(-\frac{5}{6})=\frac{1}{6}
\end{align}$$
Hence, the area of the the shaded region i $O=O_1+O_2=\frac{5}{6}+\frac{1}{6}=1$.

