Definition: Consider the function $f(x)$ on the interval $[a,b]$.
We can relate the notion of an integral to the area of a region below the graph of a function.
Theorem:
- The function $f(x)$ is non-negative on the interval $[a,b]$ if $f(x)\geq 0$ for every $x\in[a,b]$;
- The function $f(x)$ is non-positive on the interval $[a,b]$ if $f(x)\leq 0$ for every $x\in[a,b]$.
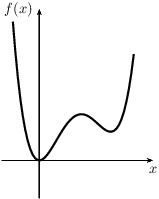 |
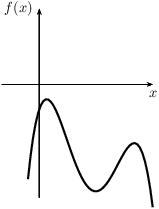 |
| non-negative function | non-positive function |
We can relate the notion of an integral to the area of a region below the graph of a function.
Theorem:
- If $f(x)$ is a non-negative function, then the area of the region enclosed by the graph of the function $f(x)$, the $x$-axis and the lines $x=a$ and $x=b$, is equal to the integral of $f(x)$ over the interval $[a,b]$, $O(f,a,b)=\int_a^b f(x)dx$;
- If $f(x)$ is a non-positive function, then the area of the region enclosed by the graph of the function $f(x)$, the $x$-axis and the lines $x=a$ and $x=b$, is equal to minus the integral of $f(x)$ over the interval $[a,b]$, $O(f,a,b)=-\int_a^b f(x)dx$.

