We bepalen de extrema van $y(x)=-2x^3+3x^2+12x+5$ voor $-5 \leq x \leq 5$.
Daarvoor gebruiken we een vijf-stappenplan.
Stap 1: $y'(x)$ bepalen
$y'(x)=-6x^2+6x+12$.
Stap 2: Stationaire punten vinden
$$\begin{align}
y'(x)=0 &\Leftrightarrow -6x^2+6x+12=0\\
&\Leftrightarrow x^2-x-2=0\\
&\Leftrightarrow (x-2)(x+1)=0\\
&\Leftrightarrow x=-1 \mbox{ of } x=2.
\end{align}$$
Stap 3: Tekenoverzicht $y'(x)$
$y'(-3)=-60$, $y'(0)=12$ en $y'(3)=-24$.
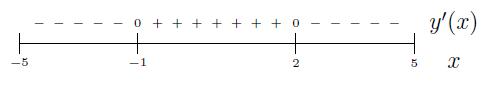
Stap 4: Extremumlocatie bepalen
$x=-5$ is een maximumlocatie
$x=-1$ is een minimumlocatie
$x=2$ is een maximumlocatie
$x=5$ is een minimumlocatie
Stap 5: Extremum bepalen
$y(-5)=270$
$y(-1)=-3$
$y(2)=25$
$y(5)=-110$
Conclusie
$y(-5)=270$ is een randmaximum
$y(-1)=-3$ is een minimum
$y(2)=25$ is een maximum
$y(5)=-110$ is een randminimum
Opmerking bij filmpje: Rond 2.50 wordt per abuis een '2' gebruikt in plaats van een '12'.
Daarvoor gebruiken we een vijf-stappenplan.
Stap 1: $y'(x)$ bepalen
$y'(x)=-6x^2+6x+12$.
Stap 2: Stationaire punten vinden
$$\begin{align}
y'(x)=0 &\Leftrightarrow -6x^2+6x+12=0\\
&\Leftrightarrow x^2-x-2=0\\
&\Leftrightarrow (x-2)(x+1)=0\\
&\Leftrightarrow x=-1 \mbox{ of } x=2.
\end{align}$$
Stap 3: Tekenoverzicht $y'(x)$
$y'(-3)=-60$, $y'(0)=12$ en $y'(3)=-24$.
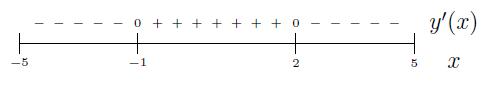
Stap 4: Extremumlocatie bepalen
$x=-5$ is een maximumlocatie
$x=-1$ is een minimumlocatie
$x=2$ is een maximumlocatie
$x=5$ is een minimumlocatie
Stap 5: Extremum bepalen
$y(-5)=270$
$y(-1)=-3$
$y(2)=25$
$y(5)=-110$
Conclusie
$y(-5)=270$ is een randmaximum
$y(-1)=-3$ is een minimum
$y(2)=25$ is een maximum
$y(5)=-110$ is een randminimum
Opmerking bij filmpje: Rond 2.50 wordt per abuis een '2' gebruikt in plaats van een '12'.

